LIBRETA DIGITAL

BACHILLERATO GENERAL MILITARIZADO

"1ER ESCUADRON DE LANCEROS DE AGUASCALIENTES"

Nombre de la Materia

MATEMATICAS

Nombre del estudiante (s)

OLIVARES HERNANDEZ VICTOR HAZEL

LUJAN LEMUS LUIS YHOSUE

CRUZ IBARRA SERGIO IVAN

CASTILLO ARELLANO OSCAR NOE

CEDILLO VELASCO DAMIAN ALEJANDRO

DOMINGUEZ VICENCIO KEVIN ZADKIEL

 

Nombre de la actividad

Blog -   libreta digital

Nombre del profesor

LORENA MARTINEZ

Fecha de entrega:

02 de Diciembre del 2022

CLASIFICACION DE NUMEROS ( NATURALES,REALES E IMAGINARIOS ETC )

¿QUE SON LOS NUMEROS NATURALES , REALES E IMAGINARIOS Y PARA QUE NOS SIRVEN ?

Los números imaginarios pueden ser positivos o negativos. Los números reales sólo pueden ser positivos o cero (el cero no es realmente un número). Los números imaginarios son un nuevo tipo de número que nos ayuda a resolver ecuaciones algebraicas

Los números Reales, se denotan con la letra (R) y se definen como el conjunto de números que agrupa o incluye los números naturales (N), enteros (Z), racionales (Q) e irracionales (I). También se puede decir, que cualquier número racional o irracional es un número real, R = Q ∪ I.

¿Cuáles son las clasificaciones de los números?

NÚMEROS REALES

1. Clasificación Números Reales.
2. Números Naturales.
3. Números Enteros.
4. Números Racionales.
5. Números Irracionales.

OPERACIONES FUNDAMENTALES

LEY DE LOS SIGNOS 

¿Qué es la ley de los signos y para que nos sirve?

Las ley de los signos se usa para resolver operaciones matemáticas como: suma, resta, multiplicación o división y consiste en saber cual será el procedimiento a seguir en cada operación donde se involucren tanto números positivos como números negativos; para de ésta manera poder llegar a un resultado correcto; debido a que debemos saber si en algunos casos sumaremos o restaremos y en otros casos si el resultado que obtengamos tendrá un signo positivo o un signo negativo.

OPERACIONES CON FRACCIONES MAXIMO Y MINIMO DENOMINADOR

 ¿Qué es la jerarquía de operaciones?  

La jerarquización o jerarquía de operaciones es el orden correcto en que se interpretan expresiones aritméticas que contienen varias operaciones. Esta nos dicta cuáles deben hacerse primero, de modo que el resultado sea el correcto.

https://blog.unitips.mx/jerarquia-de-operaciones

 

Para el cálculo de la/s solución/es de un sistema de ecuaciones lineales con dos incógnitas existen tres métodos a seguir:

 1) Reducción. 2) Igualación. 3) Sustitución

				NOTA : NO SE PUEDE PASAR UNA DIVISIÓN AL OTRO LADO CON SU OPERACIÓN CONTRARIA SI NO ESTA DIVIDIENDO A TODOS LOS MIEMBROS

¿

 

 

 

 

PLANTEAMIENTO   Se expone la aplicación del triángulo de Pascal en el desarrollo del binomio de Newton   BINOMIO DE NEWTON   El teorema del binomio, también llamado binomio de Newton expresa la enésima  potencia de un binomio como un polinomio. El desarrollo del binomio  posee singular importancia ya que aparece con mucha frecuencia en Matemáticas y posee diversas aplicaciones en otras áreas del conocimiento.   Si el binomio de la forma  se multiplica sucesivamente por sí mismo se obtienen las siguientes potencias: + De los desarrollos anteriores, se observa que:   ·          El desarrollo de   tiene  términos. 0. 6 +¿2nm, ·       El exponente de  empieza con  en el primer término y va disminuyendo en uno con cada término, hasta cero en el último. ·       El exponente de  empieza con cero en el primer término y va aumentando en uno con cada término, hasta  en el último. ·       Para cada término la suma de los exponentes de  y  es . ·       El coeficiente del primer término es uno y el del segundo es . ·          El coeficiente de un término cualquiera es igual al producto del coeficiente del término anterior por el exponente de  dividido entre el número que indica el orden de ese término. ·          Los términos que equidistan de los extremos tienen coeficientes iguales.     TRIÁNGULO DE PASCAL   El triángulo de Pascal es un esquema que tiene como característica que cada uno de los componentes de sus filas representa los coeficientes del desarrollo binomial.   Se construye de la siguiente manera: Productos notables • Un binomio al cuadrado (suma) es igual al cuadrado del primer término, más el doble producto del primero por el segundo EJEMPLO: a²+2ab+b²  • Si el termino con signo negativo esta escrito primero se deben reacomodar para que se escriba primero el positivo EJEMPLO:(a-b)²=a²+2ab+b² Representación de binomio cuadrado SISTEMA DE ECUACIONES LINEALES 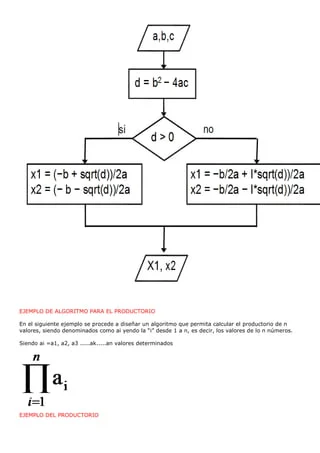DIAGRAMA DE FLUJO Y PROCESO DE RESOLUCIÓN POR REDUCCIÓN  Inicio Leer x, V, n al1-0;a12-0;a22=n; b1=0: b2=0: ¡=1:n all=a11+x (i) ^2; a12=a12+x (i); a21=a12; b1=b1+x (j)*v (i); b2=b2+y (j); a= (b1*a22-b2* a12)/ (a11*a22-a21*a12); b=(b2*a11-b1*a21)/(A11*A22-A21*A12); Escribir a, b DIAGRAMA DE FLUJO Este algoritmo presenta una manera de solucionar ecuaciones lineales de 2 variables con 2 incógnitas, el algoritmo te pide los valores de los coeficientes de las ecuaciones lineales y te retorna los valores de "x" y "y" ó un mensaje de error, según sea el caso. Resolver un sistema de ecuaciones lineales es encontrar todas sus soluciones. Los métodosde igualación, sustitución y reducción consisten en encontrar y resolver, para cada una de las incognitas, una ecuación con esa incognita y con ninguna otra ( convirtiendo así un problema dificil en uno mas facil, ¿no?). A estas ecuaciones, con solo una incognita, se llega a traves de una serie de pasos en los que las ecuaciones intermedias que se van obteniendo tienen menos incognitas que las ecuaciones previas. OPERACIONES DE FRACCIONES A PORCENTAJE ¿QUE ES? Recuerde que un porcentaje es realmente solo una forma especial de expresar una fracción como un número de 100.   Para convertir una fracción en un porcentaje, primero divida el numerador entre el denominador. Luego multiplique el decimal por 100.   ¿COMO FUNCIONA? Para convertir una fracción en un porcentaje, primero divida el numerador entre el denominador. Luego multiplique el decimal por 100.       EJEMPLO: Esto es, la fracción  puede ser convertida a un decimal al dividir 4 entre 8. Puede ser convertida en un porcentaje al multiplicar el decimal por 100. 4÷8=0.5 0.5×100=50 Así, la fracción 4/8 es equivalente a 50%    ¿COMO FUNCIONA? Para expresar un porcentaje en formato decimal, tan solo hay que dividir el número entre cien. Por ejemplo, el 5% anterior sería un 0,05. EJEMPLO: Calculamos el 25% de 120 La fracción 25/100 es 0.25 (al dividir entre 100, aparecen 2 decimales). Por tanto, el 25% de 120 es 30: 120•0.25=30 •CALCULAMOS EL 30%: Tenemos que multiplicar por 0.30: 120•0.30=36 •Calculamos el 5%: Tenemos que multiplicar por 0.05: 120•0.05=6 •Calculamos el 130%: Tenemos que multiplicar por 1.30: 120•1.30=156 Esta forma de calcular porcentajes es muy sencilla y nos permite también calcular rápidamente porcentajes de porcentajes. OPERACIONES DE DECIMALES A NOTACION CIENTIFICA: ¿QUE ES? Para escribir estos números en notación decimal, mueves el punto decimal el mismo número de lugares que el exponente. Si el exponente es positivo, mueves el punto decimal a la derecha. Si el exponente es negativo, mueves el punto decimal a la izquierda. ¿COMO FUNCIONA? Para escribir un número grande en notación científica, movemos el punto decimal a la izquierda hasta obtener un número entre 1 y 10. Como mover el punto decimal cambia el valor, es necesario multiplicar el decimal por una potencia de 10 para que la expresión conserve su valor.   EJEMPLO: PLANTEAMIENTO Se expone la aplicación del triángulo de Pascal en el desarrollo del binomio de Newton.  BINOMIO DE NEWTON El teorema del binomio, también llamado binomio de Newton expresa la enésima  potencia de un binomio como un polinomio. El desarrollo del binomio   posee singular importancia ya que aparece con mucha frecuencia en Matemáticas y posee diversas aplicaciones en otras áreas del conocimiento. Si el binomio de la forma   se multiplica sucesivamente por sí mismo se obtienen las siguientes potencias:     TRIÁNGULO DE PASCAL   El triángulo de Pascal es un esquema que tiene como característica que cada uno de los componentes de sus filas representa los coeficientes del desarrollo binomial.   Se construye de la siguiente manera:   ·       Se empieza por el 1 de la cumbre. ·          De una fila a la siguiente se escriben los números con un desfase de medio lugar o casilla para que cada casilla tenga dos números justo arriba, en la fila anterior. ·       Cada extremo de la fila tiene un 1 y el valor que se escribe en una casilla es la suma de los números que están encima. ·       Después, se efectúa una relación entre los números del triángulo de Pascal y la suma de las potencias de  , de forma que los coeficientes se asignan en el mismo orden en que aparecen.   Gráficamente esto es:    Por ejemplo, para encontrar los coeficientes del desarrollo , se le aplican los factores de la séptima fila, tal y como se muestra en la siguiente figura:       Ejemplos.   1) Aplicar el triángulo de Pascal para desarrollar    Solución.   Ubicando los coeficientes respectivos se tiene:   2) Encontrar la expansión de  aplicando el triángulo de Pascal. Solución. Ubicando los coeficientes respectivos se tiene:   CONCLUSIÓN   El triángulo de Pascal es un triángulo de números enteros, infinito y simétrico Se empieza con un  en la primera fila, y en las filas siguientes se van colocando números de forma que cada uno de ellos sea la suma de los dos números que tiene encima. La fórmula general del llamado Binomio de Newton  está formada por los coeficientes que coinciden con la línea número  del triángulo de Pascal. https://www.youtube.com/watch?v=9ri5dwV2K6E                        1.    SOLUCION POR FACTORIZACION. Como  toda ecuación  cuadrática es  equivalente a  una ecuación  en la cual uno  de sus miembros es un polinomio de segundo grado y el otro es cero; entonces, cuando el polinomio de segundo grado pueda factorizarse, se procede así:  Si ax2 + bx + c = (x + r1).(x + r2),  entonces,  la  ecuación  ax2 + bx + c = 0  es equivalente a:  (x + r1).(x + r2) = 0 (1).  La  ecuación (1)  puede resolverse usando la  propiedad del sistema de los números reales: X.Y = 0 ↔ X = 0 ν Y = 0.    2.      SOLUCION POR COMPLEMENTO DE CUADRADOS. Este método es el más antiguo que existe para encontrar las soluciones de una ecuación cuadrática.  Se supone que la ecuación: ax2 + bx + c = 0, x ≠ 0, es equivalente a la ecuación cuadrática: x2 + px = q (1).  Sumando  en ambos miembros de la ecuación (1), se obtiene:           ó         Extrayendo raíz cuadrada en ambos miembros de la última igualdad (lo cual tiene sentido solo si  4q + p2 ≥ 0), se obtiene:    ,  de donde   (2). La fórmula (2) proporciona las dos soluciones (una para cada signo) de la ecuación cuadrática (1), que es equivalente a la ecuación:  .  ax2 + bx + c = 0,    3.     SOLUCION POR FORMULA GENERAL Usando el método de completación de cuadrados, demuestre que la solución de la ecuación cuadrática: ax2 + bx + c = 0, con x ≠ 0, viene dada por :    Solución: La ecuación: ax2 + bx + c = 0, con x ≠ 0,es equivalente a la ecuación :    Sumando  ,en ambos miembros de la igualdad anterior, se obtiene:  O equivalentemente,  Extrayendo la raíz cuadrada en ambos miembros de la última igualdad(si b2-4ac ≥ 0), se obtiene:     De donde :   (2) La fórmula (2) se conoce como: fórmula general para resolver la ecuación cuadrática  ax2 + bx + c = 0, con x ≠ 0. La forma ax2 + bx + c = 0 se llama la forma estándar de una ecuación cuadrática. Antes de resolver una ecuación cuadrática usando la fórmula cuadrática, es vital estar seguros de que la ecuación tenga esta forma. Si no, podríamos usar los valores incorrectos de a, b, o c y la fórmula dará soluciones incorrectas.     Ejemplo Problema Reescribe la ecuación 3x + 2x2 + 4 = 5 en su forma estándar e identifica a, b y c.   3x + 2x2 + 4 = 5 3x + 2x2 + 4 – 5 = 5 – 5 Primero asegúrate de que el lado derecho de la ecuación sea 0. En este caso, todo lo que tienes que hacer es restar 5 de ambos lados.   3x + 2x2 – 1 = 0 2x2 + 3x – 1 = 0 Simplifica y escribe los términos con el exponente en la variable en orden descendiente.   2x2 + 3x – 1 = 0 ↓   ↓   ↓     ax2   bx   c       a = 2, b = 3, c = −1   Ahora que la ecuación está en su forma estándar, puedes leer los valores de a, b y c de los coeficientes y la constante. Observa que como la constante 1 se resta, c debe ser negativa. Respuesta 2x2 + 3x – 1 = 0; a = 2, b = 3, c = −1     Ejemplo Problema Reescribe la ecuación 2(x + 3)2 – 5x = 6 en su forma estándar e identifica a, b y c.   2(x + 3)2 – 5x = 6 2(x + 3)2 – 5x – 6 = 6 – 6 Primero asegúrate de que el lado derecho de la ecuación sea 0.   2(x2 + 6x + 9) – 5x – 6 = 0 2x2 + 12x + 18 – 5x – 6 = 0 2x2 + 12x – 5x + 18 – 6 = 0 2x2 + 7x + 12 = 0 Expande el binomio cuadrado, luego simplifica combinando términos semejantes.   Asegúrate de escribir los términos con el exponente en la variable en orden descendiente.   2x2 + 7x + 12 = 0 ↓   ↓   ↓     a   b   c       a = 2, b = 7, c = 12   Ahora que la ecuación está en su forma estándar, puedes leer los valores de a, b y c de los coeficientes y la constante. Respuesta 2x2 + 7x + 12 = 0; a = 2, b = 7, c = 12     Identifica los valores de a, b y c en su forma estándar de la ecuación 3x + x2 = 6.   A) a = 3, b = 1, c = 6 B) a = 1, b = 3, c = 6 C) a = 1, b = 3, c = −6 D) a = 3, b = 1, c = −6   Mostrar/Ocultar Respuesta       Derivando la fórmula cuadrática   Completemos el cuadrado en la ecuación general para ver exactamente cómo se produce la fórmula cuadrática. Recuerda el proceso de completar el cuadrado.   ·         Empieza con una ecuación de la forma x2 + bx + c = 0.   ·         Reescribe la ecuación de modo que x2 + bx quede despejado a un lado. ·         Completa el cuadrado sumando a ambos lados. ·         Reescribe el trinomio cuadrado perfecto como el cuadrado de un binomio.   ·         Usa la propiedad de la raíz cuadrada y resuelve x.   ¿Puedes completar el cuadrado en la ecuación cuadrática general ax2 + bx + c = 0? Inténtalo tú antes de continuar con el ejemplo siguiente. Pista: Observa que en la ecuación general, el coeficiente de x2 no es igual a 1. Puedes dividir la ecuación entre a, lo que hace las expresiones un poco complicadas, pero si tienes cuidado, puede salir bien y al final, ¡tendrás la fórmula cuadrática!     Ejemplo Problema Calcula el cuadrado de ax2 + bx + c = 0 para encontrar la fórmula cuadrática.     Divide entre a ambos lados de la ecuación para que el coeficiente de x2 sea 1.     Reescribe de modo que el lado izquierdo sea x2 + bx (aunque en este caso bx realmente es ).     Como el coeficiente de x es , el valor a sumar a ambos lados es .     Escribe el lado izquierdo como un binomio cuadrado.     Evalúa como .     Escribe las fracciones en el lado derecho usando un común denominador.     Suma las fracciones de la derecha.     Usa la Propiedad de la Raíz Cuadrada. ¡Recuerda que quieres las dos raíces, positiva y negativa!     Resta  de ambos lados para despejar x.       El denominador dentro del radical es un cuadrado perfecto, entonces: Respuesta   Suma las fracciones ya que tienen un común denominador.     Y ahí está, la fórmula cuadrática.     Resolviendo ecuaciones cuadráticas usando la formula cuadrática   La fórmula cuadrática funcionará con cualquier ecuación cuadrática, pero sólo si la ecuación está en la forma estándar, . Para usarla, sigue estos pasos.   ·         Pon primero la ecuación en su forma estándar.   ·         Identifica los coeficientes, a, b y c. Ten cuidado de incluir los signos negativos si los términos bx o c se restan.   ·         Sustituye los valores por los coeficientes en la fórmula cuadrática.   ·         Simplifica lo más posible.   ·         Usa el ± en frente del radical para separar la solución en dos valore: uno en el que la raíz cuadrada se suma y el otro en el que la raíz cuadrada se resta.   ·         Simplifica ambos valores para obtener las posibles soluciones.   Son bastantes pasos. Intentemos usar la fórmula cuadrática para primero resolver una ecuación relativamente simple; luego volveremos a resolver usando otro método de factorización.     Ejemplo Problema Usar la fórmula cuadrática para resolver la ecuación x2 + 4x = 5.   x2 + 4x = 5 x2 + 4x – 5 = 0   Primero escribe la ecuación en su forma estándar.     a = 1, b = 4,  c = −5   Observa que el signo de resta significa que la constante c es negativa.     Sustituye los valores en la fórmula cuadrática.         Simplifica, teniendo cuidado de usar los signos correctos.     Simplifica un poco más.       Simplifica el radical: .     o     Separa y simplifica para encontrar las soluciones de la ecuación cuadrática. Observa que en una, se suma 6 y en la otra se resta 6.. Respuesta x = 1 o −5         Puedes comprobar estas soluciones sustituyendo 1 y −5 en la ecuación original.   x = 1 x = −5 x2 + 4x = 5 x2 + 4x = 5 (1)2 + 4(1) = 5 (−5)2 + 4(−5) = 5 1 + 4 = 5 25 ‒ 20 = 5 5 = 5 5 = 5   Obtienes enunciados válidos, por lo que sabes que ambas soluciones funcionan: x = 1 o −5. ¡Has resuelto con éxito una ecuación usando la fórmula cuadrática!   Sin embargo, al ver x2 + 4x = 5, pudiste haber pensado “ya sé cómo resolver esto; puedo reescribir la ecuación como x2 + 4x – 5 = 0 y luego factorizar como (x + 5)(x – 1) = 0, entonces x = −5 o 1.” Esto es correcto, ¡y felicidades si encontraste esta conexión!   Algunas veces, podría ser más fácil resolver una ecuación usando los métodos convencionales de factorización, como encontrar números pares que se suman a un número (en este ejemplo, 4) y que producen una cantidad específica (en este ejemplo, −5) cuando se multiplican. El poder de la fórmula cuadrática es que puede usarse para resolver cualquier ecuación cuadrática, incluso aquellas donde no se puede encontrar el número de combinaciones.   La mayoría de las ecuaciones cuadráticas que hemos visto han tenido dos soluciones, como la anterior. El siguiente ejemplo es un poco distinto.     Ejemplo Problema Usa la fórmula cuadrática para resolver la ecuación x2 – 2x = 6x – 16.   x2 – 2x = 6x – 16 x2 – 2x – 6x + 16 = 0 x2 – 8x + 16 = 0   Resta 6x de cada lado y suma 16 a ambos lados para poner la ecuación en su forma estándar.           Identifica los coeficientes a, b y c. x2 = 1x2, entonces a = 1. Como 8x se resta, b es negativo.   a = 1, b = −8, c = 16                 Sustituye los valores en la fórmula cuadrática.         Simplifica.       Como la raíz cuadrada de 0 es 0 y sumar o restar 0 da el mismo resultado, sólo hay un valor posible. Respuesta x = 4         De nuevo, comprueba usando la ecuación original.   x2 – 2x = 6x – 16 (4)2 – 2(4) = 6(4) – 16 16 – 8 = 24 – 16 8 = 8   Intentemos un último ejemplo. Este también tiene una diferencia en la solución.     Ejemplo Problema Usa la fórmula cuadrática para resolver la ecuación x2 + 2x = −5.   x2 + 2x = −5 x2 + 2x + 5 = 0   Primero escribe la ecuación en su forma estándar.     a = 1, b = 2,  c = 5             Sustituye los valores en la fórmula cuadrática.         Simplifica, teniendo cuidado con los signos.     Simplifica un poco más.       Simplifica el radical, ¡pero observa que el número dentro del radical es negativo! La raíz cuadrada de −16 es imaginaria. .     o     Separa y simplifica para encontrar las soluciones de la ecuación cuadrática. Respuesta x = −1 + 2i o −1 – 2i         Comprueba estas soluciones en la ecuación original. Ten cuidado cuando expandes los cuadrados y reemplazas i2 con -1.   x = −1 + 2i x = −1 – 2i x2 + 2x = −5 x2 + 2x = −5 (−1+2i)2 + 2(−1 + 2i) = −5 (−1 – 2i)2 + 2(−1 – 2i) = −5 1 – 4i + 4i2 – 2 + 4i = −5 1 + 4i + 4i2 – 2 – 4i = −5 1 – 4i + 4(−1) – 2 + 4i = −5 1 + 4i + 4(-1) – 2 – 4i = −5 1 – 4 – 2 = −5 1 – 4 – 2 = −5 −5 = −5 −5 = −5     Usa la fórmula cuadrática para resolver la ecuación x2 – 2x – 4 = 0.   A) x = 2 B) x =11, x = −9 C) ,  D) ,    Mostrar/Ocultar Respuesta       El discriminante   Estos ejemplos han mostrado que una ecuación cuadrática puede tener dos soluciones reales, una solución real, o dos soluciones complejas.   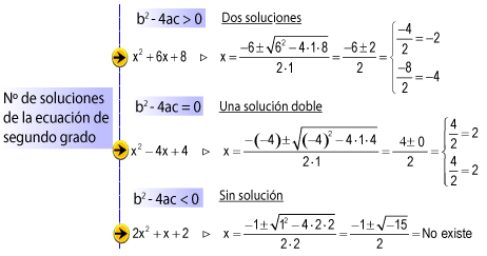En la fórmula cuadrática, la expresión dentro del símbolo radical determina el número y tipo de soluciones que dará la fórmula. Esta expresión, b2 – 4ac, se llama el discriminante de la ecuación ax2 + bx + c = 0.   Pensemos sobre cómo afecta el discriminante la evaluación de  y cómo ayuda a determinar el conjunto solución.   ·         Si b2 – 4ac > 0, entonces el número dentro del radical será un valor positivo. Siempre puedes encontrar la raíz cuadrada de un positivo, por lo que evaluar la fórmula cuadrática resultará en dos soluciones reales (una sumado la raíz cuadrada positiva y la otra restando).   ·         Si b2 – 4ac = 0, entonces sacarás la raíz cuadrada de 0, que es 0. Como sumar y restar 0 da el mismo resultado, la porción "±" de la fórmula no importa. Habrá una solución real.   ·         Si b2 – 4ac < 0, entonces el número dentro del radical será un valor negativo. Como no puedes encontrar la raíz cuadrada de un número negativo usando números reales, no habrá soluciones reales. Sin embargo, puedes usar números imaginarios. Entonces tendrás soluciones complejas, una sumando la raíz cuadrada imaginaria y la otra restando.     Ejemplo Problema Usa el discriminante para determinar cuántas soluciones hay y de qué tiempo de la ecuación cuadrática x2 – 4x + 10 = 0.     b2 – 4ac (−4)2 – 4(1)(10) Evalúa b2 – 4ac. Primero observa que a = 1, b = −4 y c = 10.   16 – 40 = −24 El resultado es un número negativo. El discriminante es negativo, por lo que la ecuación cuadrática tiene dos soluciones complejas. Respuesta La ecuación cuadrática x2 – 4x + 10 = 0 tiene dos soluciones complejas.                  Existe una técnica llamada fórmula general para resolver ecuaciones cuadráticas de segundo grado que funciona con cualquier ecuación. Puedes resolver una ecuación cuadrática completando el cuadrado, reescribiendo parte de la ecuación como un trinomio cuadrado perfecto. Si completas el cuadrado de una ecuación genérica ax2 + bx + c = 0 y luego resuelves x, encuentras que  esta ecuación se le conoce como ecuación cuadrática. Esta fórmula es muy útil para resolver ecuaciones cuadráticas que son difíciles o imposibles de factorizar y usarla puede ser más rápido que completar el cuadrado. La fórmula cuadrática puede usarse para resolver cualquier ecuación de la forma ax2 + bx + c = 0.  Recuerda que una raíz cuadrada posee siempre dos valores, uno positivo y uno negativo. De manera que cuando utilices la fórmula general debes completar ambos signos por separado. DE DÓNDE SALE LA ECUACIÓN GENERAL NOTA: En la fórmula general al radicando de la raíz se le denomina discriminante de la ecuación, el discriminante proporciona información valiosa acerca de las soluciones: Expresiones       Enunciado Términos                    Composición  Constante o lateral          a, b, c ,d                                                       Constante o lateral            a, b, c ,d

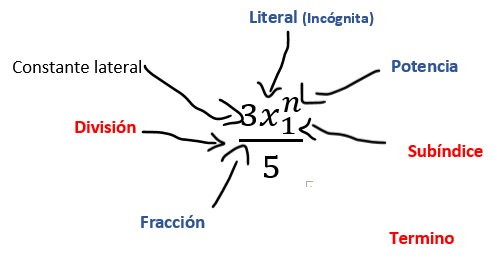
 Operaciones, símbolos e incógnita

Qué es una sucesión?

Una sucesión es un conjunto de cosas (normalmente números) en un cierto orden.

 

 

Finita o infinita

Si la sucesión sigue para siempre, es una sucesión infinita,
si no es una sucesión finita

Ejemplos:

{1, 2, 3, 4 ,...} es una sucesión muy simple (y es una sucesión infinita)

{20, 25, 30, 35, ...} también es una sucesión infinita

{1, 3, 5, 7} es la sucesión de los 4 primeros números impares (y es una sucesión infinita)

{4, 3, 2, 1} va de 4 a 1 hacia atrás

{1, 2, 4, 8, 16, 32, ...} es una sucesión infinita donde vamos duplicando cada término

{a, b, c, d, e} es la sucesión de las 5 primeras letras en order alfabético

{a, l, f, r, e, d, o} es la sucesión de las letras en el nombre "alfredo"

{0, 1, 0, 1, 0, 1, ...} es la sucesión que alterna 0s y 1s (sí, siguen un orden, en este caso un orden alternativo)

En orden

Cuando decimos que los términos están "en orden", ¡nosotros somos los que decimos qué orden! Podría ser adelante, atrás... o alternando... ¡o el que quieras!

Como un conjunto

Una sucesión es muy parecida a un conjunto, pero:

• los términos están en orden (en los conjuntos el orden no importa).
• el mismo valor puede aparecer muchas veces (en los conjuntos solo una vez).

Ejemplo: {0, 1, 0, 1, 0, 1, ...} es la sucesión que alterna 0s y 1s.

El conjunto sería solo {0,1}

Notación

Las secuencias también usan la misma notación que los conjuntos: se enumera cada elemento, separados por una coma, y luego se ponen llaves alrededor de todo.

{3, 5, 7, ...}

Los corchetes { } también se conocen como "llaves".

La regla

Una sucesión sigue una regla que te dice cómo calcular el valor de cada término.

Ejemplo: la sucesión {3, 5, 7, 9, ...} empieza por 3 y salta 2 cada vez:

¡Pero la regla debería ser una fórmula!

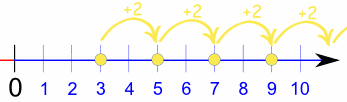
Decir que "empieza por 3 y salta 2 cada vez" no nos dice cómo se calcula el:

• 10º término,
• 100º término, o
• n-ésimo término (donde n puede ser cualquier número positivo que queramos).

Así que queremos una fórmula con "n" dentro (donde n será la posición que tiene el término).

Entonces, ¿cuál sería la regla para {3, 5, 7, 9, ...}?

Primero, vemos que la sucesión sube 2 cada vez, así que podemos adivinar que la regla va a ser "2 × n". Vamos a verlo:

Probamos la regla: 2n

n	Término	Prueba
1	3	2n = 2×1 = 2
2	5	2n = 2×2 = 4
3	7	2n = 2×3 = 6

Esto casi funciona... pero la regla da todo el tiempo valores 1 unidad menos de lo que debería, así que vamos a cambiarla un poco:

Probamos la regla: 2n+1

n	Término	Regla
1	3	2n+1 = 2×1 + 1 = 3
2	5	2n+1 = 2×2 + 1 = 5
3	7	2n+1 = 2×3 + 1 = 7

¡Funciona!

Así que en vez de decir "empieza por 3 y salta 2 cada vez" escribimos la regla como

2n+1

Ahora, por ejemplo, podemos calcular el término 100º:

2 × 100 + 1 = 201

Muchas Reglas

Pero las matemáticas son tan poderosas que podemos encontrar más de una regla que funcione para cualquier sucesión.

Ejemlpo: la sucesión {3, 5, 7, 9, ...}

Acabamos de mostrar que la regla para {3, 5, 7, 9, ...} es: 2n+1

Y obtuvimos: {3, 5, 7, 9, 11, 13, ...}

¿Pero podemos encontrar otra regla?

¿Qué tal "números impares que no tengan un 1 en sus dígitos"?:

Tendríamos: {3, 5, 7, 9, 23, 25, ...}

¡Una sucesión completamente diferente!

Y podríamos encontrar más reglas que coincidan con {3, 5, 7, 9, ...}. ¡De verdad!

Por lo tanto, es mejor decir "Una regla" en lugar de "La regla" (a menos que sepamos que es la regla correcta).

Notación

Para que sea más fácil escribir las reglas, normalmente lo hacemos así:

xn es el término n es la posición de ese término

Ejemplo: Para hablar del "quinto término" sólo tienes que escribir: x5

Entonces podemos escribir una regla para {3, 5, 7, 9, ...} en forma de ecuación, así:

xn = 2n+1

Ahora, si queremos calcular el 10º término, podemos escribir:

x10 = 2n+1 = 2×10+1 = 21

¿Puedes calcular el 50º término? ¿Y el 500º?

Aquí está otro ejemplo:

Ejemplo: Calcula los primeros 4 términos de esta sucesión:

{an} = { (-1/n)n }

Operaciones:

• a1 = (-1/1)1 = -1
• a2 = (-1/2)2 = 1/4
• a3 = (-1/3)3 = -1/27
• a4 = (-1/4)4 = 1/256

Respuesta:

{an} = { -1, 1/4, -1/27, 1/256, ... }

Sucesiones especiales

Ahora veamos algunas sucesiones especiales y sus reglas:

Sucesiones aritméticas

El ejemplo que acabamos de usar, {3,5,7,9,...}, es una sucesión aritmética (o progresión aritmética), porque la diferencia entre un término y el siguiente es una constante.

Ejemplos

1, 4, 7, 10, 13, 16, 19, 22, 25, ...

Esta sucesión tiene una diferencia de 3 entre cada dos términos.
La regla es xn = 3n−2

En general, podemos escribir una sucesión aritmética de esta forma:

{a, a+d, a+2d, a+3d, ... }

donde:

• a es el primer término, y
• d es la diferencia entre los términos (llamada "diferencia común")

Y podemos establecer la regla:

xn = a + d(n-1)

(Usamos "n-1" porque la d no se usa en el primer término).

Sucesiones geométricas

En una sucesión geométrica cada término se calcula multiplicando el anterior por una constante.

Ejemplos:

2, 4, 8, 16, 32, 64, 128, 256, ...

Esta sucesión tiene un factor 2 entre cada dos términos.
La regla es xn = 2n

En general, podemos escribir una sucesión geométrica de esta forma:

{a, ar, ar2, ar3, ... }

donde:

• a es el primer término, y
• r es la proporción entre cada par de términos (llamada "razón común")

Nota: r no puede ser 0.

• Cuando r=0, obtenemos la sucesión {a,0,0,...}, la cual no es geométrica.

Y la regla es:

xn = ar(n-1)

(Usamos "n-1" porque ar0 es el 1er término)