El método de Gauss consiste en transformar un sistema de ecuaciones en otro equivalente de forma que éste sea escalonado.

Obtenemos sistemas equivalentes por eliminación de ecuaciones dependientes. Si:

Todos los coeficientes son ceros.

Dos filas son iguales.

Una fila es proporcional a otra.

Una fila es combinación lineal de otras.

Criterios de equivalencia de sistemas de ecuaciones

1º

Si a ambos miembros de una ecuación de un sistema se les suma o se les resta una misma expresión, el sistema resultante es equivalente.

2º

Si multiplicamos o dividimos ambos miembros de las ecuaciones de un sistema por un número distinto de cero, el sistema resultante es equivalente.

3º

Si sumamos o restamos a una ecuación de un sistema otra ecuación del mismo sistema, el sistema resultante es equivalente al dado.

4º

Sin en un sistema se sustituye una ecuación por otra que resulte de sumar las dos ecuaciones del sistema previamente multiplicadas o divididas por números no nulos, resulta otro sistema equivalente al primero.

5º

Si en un sistema se cambia el orden de las ecuaciones o el orden de las incógnitas, resulta otro sistema equivalente.

Método de Gauss

El método de Gauss consiste en utilizar el método de reducción de manera que en cada ecuación
tengamos una incógnita menos que en la ecuación precedente.

El sistema transformado en matriz:

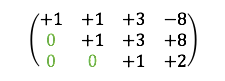
Si te fijas, ya podemos despejar directamente una de las incógnitas. Por tanto, este tipo de sistemas es muy fácil de resolver obteniendo el valor de las incógnitas de abajo hacia arriba. De esta manera, podemos ir sustituyendo los valores obtenidos en las anteriores.

z=2

Sustituimos el valor de “z” en la segunda ecuación y obtenemos el valor de “y”:

y+3.(2)=8;

 y=8-6=2
y=+2

Sustituimos el valor de “z” e “y” en la primera ecuación y obtenemos “x”:

 y=2

x+(2)+3.(2)=-8;

 x=-16

Si nuestro sistema no es un sistema escalonado, lo podemos resolver mediante el método de Gauss. El método consiste en  “hacemos cero”, es decir, sometemos a las ecuaciones a transformaciones elementales:

• Multiplicamos por un número distinto de cero.
• Sumar una ecuación a otra multiplicada por un número.

Para trabajar mejor utilizamos sólo los números (coeficientes y término independiente) y trabajamos con una estructura de matriz.

Ejemplo:

Utilizamos los coeficientes y los términos independientes y realizamos una matriz:

Necesitamos hacer ceros en los números destacados en la matriz anterior.

Primeras transformaciones, deseamos realizar los ceros de la primera columna:

Primer paso, transformar la segunda fila,

1. Fila uno multiplicada por -3

-3.(+1 +1 +1 +2)=-3 -3 -3 -6

2. Le sumo la fila 2.

Segundo paso, transformar la tercera fila,

1. Fila uno multiplicada por +2.

+2.(+1 + 1+1 +2 )=+2 +2 +2 +4

2. Le sumo la fila 3.

Así, la matriz resultante sería:

Segundas transformaciones, deseamos realizar el ceros de la segunda columna:

Para ello, sólo utilizamos la segunda y tercera fila:

1. Fila uno se mantiene.
2. Fila dos se multiplica por 3.

+3.(0 -5 -4 -2)=+0 -15 -12 -6

3. Fila tres se multiplica por 5.

+5.(0 +3 +4 +6)=0 +15 +20 +30

4. Sumo la fila dos y tres transformadas.

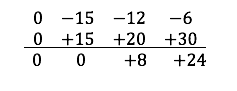
De esta manera, el sistema resulta:

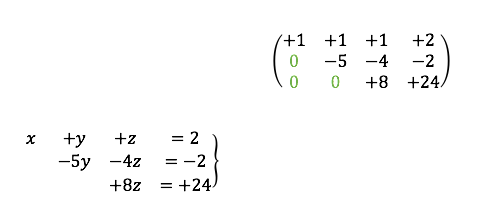
Siendo la solución:

z=24/8=+3

z=+3

Sustituimos el valor de “z” en la segunda ecuación y obtenemos el valor de “y”:

-5y-4.3=-2
-5y=-2+12
y=+10/-5=-2

 y=-2

Sustituimos el valor de “z” e “y” en la primera ecuación y obtenemos “x”:

x+(-2)+3=+2

x=+2-3+2

x=+1

Puedes ver otro ejercicio resuelto en este videotutorial: